Исследование чисел натурального ряда (ПОК)
В этой статье представлены некоторые результаты исследований, связанных с применением нового способа умножения, который изобретён к. ф.н. Василием Ивановичем Оконешниковым. Учёный утверждает, что человек способен запоминать огромный запас информации, главное – как эту информацию расположить. Лучший вариант - это девятеричная система. Все данные располагают в девяти ячейках, как в кнопках калькулятора.
Напомним суть этой новой процедуры (манипуляции),, придуманной ОКОНЕШНИКОВЫМ В. И., которую далее будем для краткости именовать по имени создателя ПОК. А затем, пойдём дальше.
Суть и ОПИСАНИЕ ПОК
Считать по такой таблице очень просто.
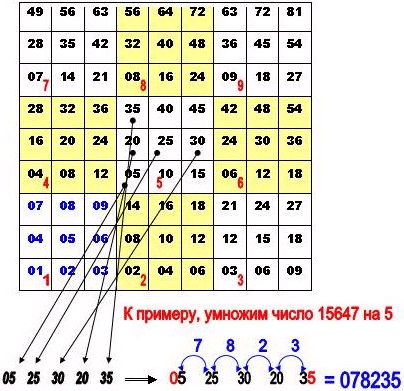
Например, надо умножить число 15647 на 5,
- Прежде всего, уточним, что число 15647 – множимое, а цифра 5 - множитель.
- С помощью цифр множителя (5) определяется (выбирается) малый квадрат (3х3 ячейки) из которого далее будут выписываться в один ряд числа.
- Цифры множимого (в порядке их обычного чтения) – это указатели на те ячейки, из которых поочерёдно делаются выписки в ряд.
- Из малой ячейки, которая соответствует множителю, т.е. пятёрке 5 (см. красные большие числа в квадратах 3х3), выбираем числа, соответственно цифрам множимого (15647) - числа по порядку: то есть единице, пятёрке, шестёрке, четвёрке и семёрке.
- Получаем специально выписанный ряд чисел : 05 25 30 20 35
- Почему именно эти числа? Потому, что каждый из малых квадратов (3х3) имеет постоянную и одинаковую нумерацию. Порядок нумерации ячеек здесь такой: из левого нижнего угла (это = 1) направо - по нижней строке, затем переход в левую клетку средней строки (это цифра = 4) и так далее. Получается обход «Змейкой»
- Левая цифра (самого первого) числа, выписанного из ячейки №5, на которые указала первая из всех разрядов цифра «множимого» (у нас - ноль) оставляется без изменений, а следующие складываотся, как это показано на отдельном рисунке в самом низу.
- Последняя цифра из выписанного ряда чисел также оставляется без изменений.
 |
Если же при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.
Из нового метода (ПОК) мы позаимствуем оригинальный метод формирования итогового результата, а именно сложение с определённым принципом группировки цифр слагаемых чисел (см. иллюстрацию выше).
Данное исследование относится к области эзотерической математики.
Естественным образом эзотерическая математика никак не могла обойтись без Первоцифр. Мы не знаем, сегодня, как именно трактовались и понимались Первоцифры нашими древними предками. Естественно предполагать, что они могли находить и использовать необычные свойства Первоцифр и чисел.
По этой причине мы пытаемся сейчас использовать нетрадиционные манипуляции для того, чтобы нащупать упомянутые неизвестные свойства.
Процедура Василия Оконешникова (ПОК) имеет нетрадиционное действие, который вкупе с другими правилами действия привёл к открытию нового способа умножения. Исследованию этого нового способа умножения было уже посвящено несколько моих работ…….
В данном исследовании я воспользуюсь упомянутым нетрадиционным способом действием ПОК по группировке и сложению цифр числовых рядов с получением новых чисел, которые затем исследуются дополнительно.
Итак, объект исследования - натуральный ряд чисел (цифр).
Правило №1 – исследуются интервалы между каждой парой смежных цифр (чисел).Для этого первые цифры вводятся в рассмотрение с дополнительными нулями, что превращает их в числа и позволяет применить к ним ПОК.
Правило №2 Согласно ПОК каждая пара чисел отражает собой интервал между числами. Выписанные рядом два числа, например, (12 – 13) позволяют сгруппировать среднюю часть 1(2 – 1)3 и вычислить её сумму (2+1) =3. Далее получается трёхзначное , новое число 133, которое анализируется в соотношении с другими, подобными числами.
Правило №3. Анализ новых чисел, полученных применением ПОК, включает в себя:
- Установление систематической разницы (дельты) между числами
- Поиск простых чисел
- Поиск констант
Данные исследования представлены в Таблице 1 ниже.
№Х
п/п |
Интервал
смежных чисел
(начало-конец) |
Процедура
«пОк» |
Результат
пОк |
NUM |
Дельта
N (X+1) - NX
11 = Const |
Место
простых
чисел |
| 00 |
Нет
интервала? |
0(0-0)0 |
000 |
0 |
нет |
? |
| 01 |
00-01 |
0(0-0)1 |
001 |
2 |
001-000=1 |
1 |
| 02 |
01-02 |
0(1-0)2 |
012 |
3 |
012-001=011 |
3х4 |
| 03 |
02-03 |
0(2-0)3 |
023 |
5 |
023-012=011 |
23 |
| 04 |
03-04 |
0(3-0)4 |
034 |
7 |
011 |
2х17 |
| 05 |
04-05 |
0(4-0)5 |
045 |
9 |
011 |
5х9 |
| 06 |
05-06 |
0(5-0)6 |
056 |
2 |
011 |
7х8 |
| 07 |
06-07 |
0(6-0)7 |
067 |
4 |
011 |
67 |
| 08 |
07-08 |
0(7-0)8 |
078 |
6 |
011 |
6х13 |
| 09 |
08-09 |
0(8-0)9 |
089 |
8 |
011 |
89 |
| 10 |
09-10 |
0(9-1)0 |
100 |
1 |
11 |
5х20 |
| 11 |
10-11 |
1(0-1)1 |
111 |
3 |
11 |
3х37 |
| 12 |
11-12 |
1(1-1)2 |
122 |
5 |
11 |
2х61 |
| 13 |
12-13 |
1(2-1)3 |
133 |
7 |
11 |
7х19 |
| 14 |
13-14 |
1(3-1)4 |
144 |
9 |
11 |
3х48 |
| 15 |
14-15 |
1(4-1)5 |
155 |
2 |
11 |
5х31 |
| 16 |
15-16 |
1(5-1)6 |
166 |
4 |
11 |
2х83 |
| 17 |
16-17 |
1(6-1)7 |
177 |
6 |
11 |
3х59 |
| 18 |
17-18 |
1(7-1)8 |
188 |
8 |
11 |
4х47 |
| 19 |
18-19 |
1(8-1)9 |
199 |
1 |
11 |
199 |
| 20 |
19-20 |
1(9-2)0 |
210 |
3 |
11 |
7х30 |
| 21 |
20-21 |
2(0-2)1 |
221 |
5 |
11 |
221 |
| 22 |
21-22 |
2(1-2)2 |
232 |
7 |
11 |
8х29 |
| 23 |
22-23 |
2(2-2)3 |
243 |
9 |
11 |
3х81 |
| 24 |
23-24 |
2(3-2)4 |
254 |
2 |
11 |
2х127 |
| 25 |
24-25 |
2(4-2)5 |
265 |
4 |
11 |
5х53 |
| 26 |
25-26 |
2(5-2)6 |
276 |
6 |
11 |
12х23 |
| 27 |
26-27 |
2(6-2)7 |
287 |
8 |
11 |
7х41 |
| 28 |
27-28 |
2(7-2)8 |
298 |
1 |
11 |
2х149 |
| 29 |
28-29 |
2(8-2)9 |
309 |
3 |
11 |
3х103 |
| 30 |
29-30 |
2(9-3)0 |
320 |
5 |
11 |
5х64 |
| 31 |
30-31 |
3(0-3)1 |
331 |
7 |
11 |
331 |
| 32 |
31-32 |
3(1-3)2 |
342 |
9 |
11 |
18х19 |
| 33 |
32-33 |
3(2-3)3 |
353 |
2 |
11 |
353 |
| 34 |
33-34 |
3(3-3)4 |
364 |
4 |
11 |
28х13 |
| 35 |
34-35 |
3(4-3)5 |
375 |
6 |
11 |
3х125 |
| 36 |
35-36 |
3(5-3)6 |
386 |
8 |
11 |
2х193 |
| 37 |
36-37 |
3(6-3)7 |
397 |
1 |
11 |
397 |
| 38 |
37-38 |
3(7-3)8 |
408 |
3 |
11 |
24х17 |
| 39 |
39-39 |
3(9-3)9 |
419 |
5 |
11 |
419 |
| 40 |
39-40 |
3(9-4)0 |
430 |
7 |
11 |
10х43 |
| 41 |
40-41 |
4(0-4)1 |
441 |
9 |
11 |
9х7х7 |
| 42 |
41-42 |
4(1-4)2 |
452 |
2 |
11 |
4х113 |
| 43 |
42-43 |
4(2-4)3 |
463 |
4 |
11 |
463 |
| 44 |
43-44 |
4(3-4)4 |
474 |
6 |
11 |
6х79 |
| 45 |
44-45 |
4(4-4)5 |
485 |
8 |
11 |
5х97 |
| 46 |
45-46 |
4(5-4)6 |
496 |
1 |
11 |
16х31 |
| 47 |
46-47 |
4(6-4)7 |
507 |
3 |
11 |
13х39 |
| 48 |
47-48 |
4(7-4)8 |
518 |
5 |
11 |
14х37 |
| 49 |
48-49 |
4(8-4)9 |
529 |
7 |
11 |
23х23 |
| 50 |
49-50 |
4(9-5)0 |
540 |
9 |
11 |
3х180 |
| 51 |
50-51 |
5(0-5)1 |
551 |
2 |
11 |
19х29 |
| 52 |
51-52 |
5(1-5)2 |
562 |
4 |
11 |
2х281 |
Таким образом, установлено, что при сопоставлении ПОК-чисел интервалов смежных членов натурального ряда присутствует постоянная константа = 11, различающая эти интервалы.
Кроме того, установлено, что при такой структуре строения чисел натурального ряда, каждый ПОК- образ интервалов смежных чисел содержит в скрытом виде различные простые числа (или выражение, содержащее простое число) .
Иными словами, действие ПОК позволяет выявить связь (пока что, неизвестно почему) каждого натурального числа со своим персональным простым (или выражением, содержащим простым число).
Другой эксперимент, описываемый ниже, состоит в таком же исследовании, но применительно уже не к смежным числам, а тройкам смежных троек чисел.
ПОК применяется к последовательным, отдельным тройкам чисел (без «перехлёста»).
Таким образом, в поле изучения попадает по два числовых интервала. Каждые три тройки чисел образуют серии, которые проиндексированы как серии А1, А2, …АN.
Правила обработки и анализа данных в этом эксперименте те же, что и раньше.
«ПОК» для троек смежных чисел натурального ряда
| | | | | | | |
№Х
п/п |
Интервал
(начало-конец) |
Сумма
троек
(NU) |
Процедура
«ПОК» |
Результат
ПОК |
Дельта
N (X+1) - NX
333 = Const |
Место
простых
чисел |
| 00 |
00 |
|
00 |
00 |
000 = - 210 (?!) |
00 |
| А1 |
01-02-03 |
06- 6 |
0(1-0) (2-0)3 |
123 |
123-000=123 |
3х41 |
| 04-05-06 |
15- 6 |
0(4-0) (5-0)6 |
456 |
456-123=333 |
24х19 |
| 07-08-09 |
24- 6 |
0(7-0) (8-0)9 |
789 |
789-456=333 |
3х263 |
| А2 |
10-11-12 |
33- 6 |
1(0-1) (1-1)2 |
1122 |
1122-789=333 |
17х66 |
| 13-14-15 |
42- 6 |
1(3-1) (4-1)5 |
1455 |
1455-1122=333 |
3х5х97 |
| 16-17-18 |
51- 6 |
1(6-1) (7-1)8 |
1788 |
1788-1455=333 |
12х149 |
| А3 |
19-20-21 |
60- 6 |
1(9-2) (0-2)1 |
2121 |
=333 |
3х7х101 |
| 22-23-24 |
69- 6 |
2(2-2) (3-2)4 |
2454 |
=333 |
6х409 |
| 25-26-27 |
78- 6 |
2(5-2) (6-2)7 |
2787 |
=333 |
3х929 |
| А4 |
28-29-30 |
87- 6 |
2(8-2) (9-3)0 |
3120 |
=333 |
13х240 |
| 31-32-33 |
96- 6 |
3(1-3) (2-3)3 |
3453 |
=333 |
3х1151 |
| 34-35-36 |
105- 6 |
3(4-3) (5-3)6 |
3786 |
=333 |
6х631 |
| А5 |
37-38-39 |
114- 6 |
3(7-3) (8-3)9 |
4119 |
=333 |
3х1373 |
| 40-41-42 |
126- 6 |
4(0-4) (1-4)2 |
4452 |
=333 |
12х7х53 |
| 43-44-45 |
132- 6 |
4(3-4) (4-4)5 |
4785 |
=333 |
3х29х55 |
| А6 |
46-47-48 |
141- 6 |
4(6-4) (7-4)8 |
5118 |
=333 |
6х853 |
| 49-50-51 |
150- 6 |
4(9-5) (0-5)1 |
5451 |
=333 |
|
| 52-53-54 |
159- 6 |
5(2-5) (3-5)4 |
5784 |
5787-5451=333 |
24х241 |
Общие выводы по исследованию:
- Тройки смежных чисел натурального ряда (в ПОК образах) сходство и постоянство своей структуры (кроме тройки 1-2-3) и различаются на число 333!, как внутри серии, так и в отношении пограничных (между сериями) тройками.
- Не выявлено очевидной связи между опытом №1 и Опытом №2.
- Установлены суммы (ПОК-чисел) для серий:
- А1 = (123+456+789) =1368;
- А2 = (1122+1455+1788)=4365;
- А3 = (2121+2454+2787)=7362;
- А4 = (3120+3453+3786)=10359;
- А5 = (4119+4452+4785)= 13356;
- А6 = (5118+5451+5784)=16353;
- Суммы ПОК-чисел в каждой серии (А1, А2, А3 и т.д.) различны, но разница соседних сумм (взятых в порядке возрастания) является числом постоянным и равным 2997 = 333 х 9 (!), т.е. в 9 раз больше, чем различие между ПОК- числами внутри одной серии: (А2 – А1) = (А3 – А2) = (А4 – А3) = (А5 – А4) = (А6 – А5) = 2997 = 9 х 333
- Этот результат аномален, так как выражение (А2 – А1) означает, что в рассмотрение включено 6 троек чисел. Между каждой смежной тройкой ПОК-чисел различие в 333 единиц. Таким образом, между 6-ю ПОК-числами – всего 5 интервалов, на каждый из которых должно приходиться по 333 единиц. Итого должна быть разница в 5 х 333 =1665 единиц (знаменитое число Е. П. Блавадской!), а не фактическое число = 2997 = 9 х 333 (!?).
- Нумерологический анализ ПОК – чисел показывает, что последовательность (ряд) этих чисел полностью соответствует ряду саморепликации Первоцифры «2». Иными словами, ПОК над числами натурального рядом, которую мы выбрали в качестве инструмента анализа структуры натурального ряда, эквивалентна ряду «чисел-обликов» процесса саморепликации цифры 2.
- Следует отметить при этом, что при подобии (эквивалентности) результатов процедуры саморепликация цифры 2 и результатов нумерологического сокращения ПОК- чисел последовательных троек членов натурального ряда имеют в качестве объекта анализа - совершенно разные объекты! И это вызывает дальнейшие вопросы.
- Выявлена также ещё одна аномалия, как обычно связанная с нулём. Ксли установленные результаты ПОК анализа полагать правильной, то для полного порядка в её структуре, давшей «сбой» на первом числе, следовало бы считать нуль (в принятой системе анализа) равным числу - 210 (!?). А это – тоже одна из необъяснённых загадок.
- Общее резюме таково: метод ПОК (в аспекте указанном в начале статьи) работает в качестве метода исследования скрытых особенностей как отдельных чисел, так и групп чисел, что делает его перспективным для областей новой нумерологии, эзотерики и числонавтики.
|