Числонавтика
Исследование простых чисел (методом лимбов)
В данном разделе предпринята попытка исследования закономерностей и связей набора простых чисел, названных «порождающими числами» в книге А. В. Баяндина «Методологический принцип обратной связи в естествознании», изд. Института философии и права СО РАН, Новосибирск, 2003 г.
Набор исследуемых чисел: 1, 7, 11, 13, 17, 19, 23, 29, 31.
Построим Лимб-9 с этими числами, учитывая то, что первые 8 чисел (кроме 31) попарно в сумме равны 30. Это положим в основу симметричного расположения на лимбе относительно вертикали. Наверху поставим число 31.
Лимб – 9 с девятью простыми числами и суммы связей между ними.
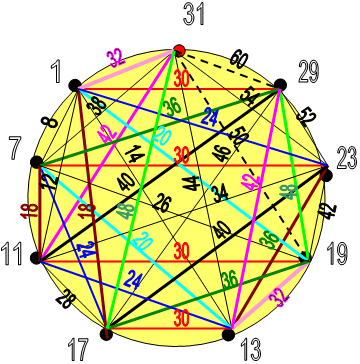 |
Общий Лимб – 9 с девятью простыми числами и суммы связей между ними, но уже в нумерологическом сокращении сумм связей, вычисленных на предыдущем Лимбе..
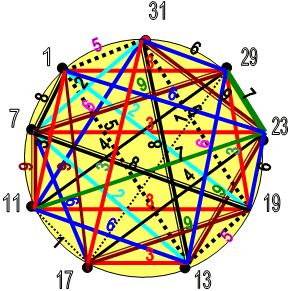 |
Выявление групп по нумерологическому признаку для формирования отдельных лимбов и последующего анализа.
Ниже отражена группировка связей между 9-тью исследуемыми простыми числами (по нумерологическому признаку).
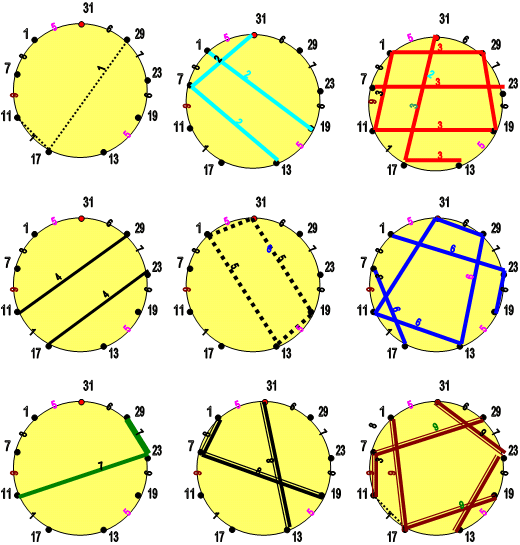 |
Рассмотрение этих лимбов показывает, что число 31 порождает связи, которые маскируют собой более отчётливые картины и поэтому, оставив только 8 первых чисел, мы получим почти те же лимбы, без ущерба для анализа. Это подтверждает картина набора лимбов, представленный ниже.
Набор лимбов, где проведено исключение всех связей с числом 31.
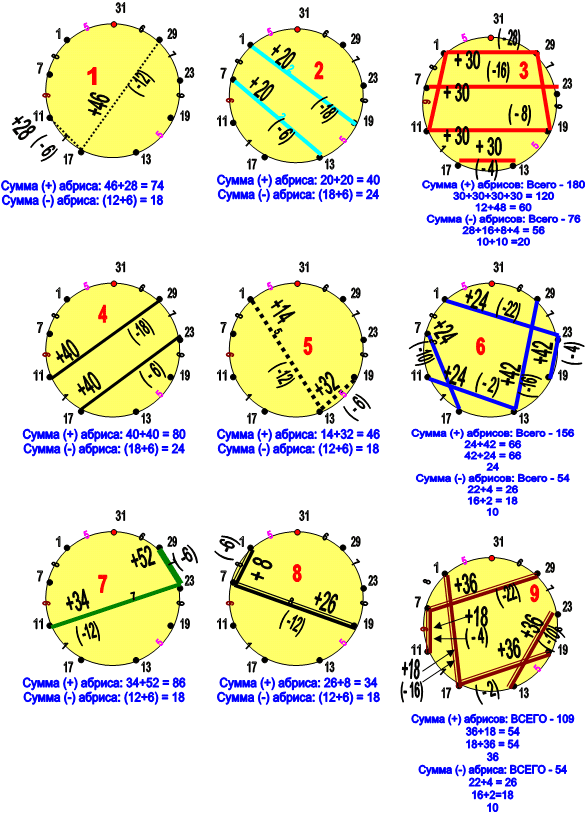
Лимбы простых чисел по группам и подсчёт сумм в нумерологических группах:
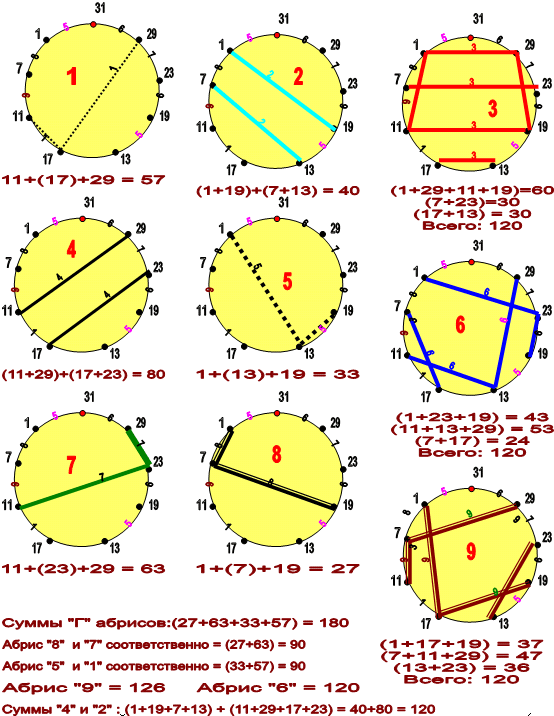 |
и суммы «-» связей, то есть - разности между связанными линиями числами (в скобках).
 |
Теперь составим обобщающую таблицу на все отдельные лимбы, классифицированные нумерологически по содержанию и виду, а также по расчётным данным.
№ № (и вид)ЛимбовNU – абриса: |
NU-1
«L» |
NU-2
«//» |
NU-3
«Д» |
NU-4
«//» |
NU-5
«L» |
NU-6
«&» |
NU-7
«L» |
NU-8
«L» |
NU-9
«&» |
| Зеркальные друг другу абрисы |
* | ++ | нет | ++ | * | + | ** | ** | + |
| Сумма связанных чисел в абрисе (>2-х) | 57 | - | 60 | - | 33 | 43 53 |
63 | 27 | 37 47 |
| Сумма не связанных чисел в абрисе | - | 20 20 |
30 30 |
40; 40 |
- | 24 | - | - | 36 |
| Общая сумма чисел в абрисах = 660 | 57 | 40 | 120 | 80 | 33 | 120 | 63 | 27 | 120 |
| Возможные группы: | 120 = (57+63) = (40+80); (33+27) = 120:2; 3х120 = 360; | ||||||||
| Разница (связанные – не связанные) | 57 | - 40 | 0 | - 80 | 0 | 72 | 63 | 27 | 48 |
| Суммарная Разница = 147 | 57- 40 + 0 – 80 + 0 + 72 + 6 3 + 27 + 48 = 147 (!) | ||||||||
| Сумма из элементов /отрезков абриса / с (+) /сумма чисел/ |
74 | 40 | 180 | 80 | 46 | 156 | 86 | 34 | 144 |
| Общая сумма (+) = 840 | S/+/ = 74+40+180+80+46+156+86+34+144 = 840 | ||||||||
| Сумма из элементов /отрезков абриса/ с (-) /разница чисел/ |
18 | 24 | 76 | 24 | 18 | 54 | 18 | 18 | 54 |
| Общая сумма (-) = 304 | S1/-/ = 18+24+76+24+18+54+18+18+54 = 304 | ||||||||
| Разница сумм (+) и (-) | 56 | 16 | 104 | 56 | 28 | 102 | 68 | 16 | 90 |
Общая сумма разниц (+ и -) = 536 |
S2/-/ = 56+16+104+56+28+102+68+16+90 = 536 S1/-/ + S2/-/ = 536 + 304 = 840 (NB! Баланс: S/+/ = S/-/ (!) | ||||||||
Числа - участники: |
11 17 29 |
1 7 13 19 |
1 7 11 13 17 19 23 29 |
11 17 23 29 |
1 13 19 |
1 7 11 13 17 19 23 29 |
11 23 29 |
1 7 19 |
1 7 11 13 17 19 23 29 |
| «ВЕС» участников: | 57 | 40 | 120 | 80 | 33 | 120 | 63 | 27 | 120 |
| Группы с весом - 120: | 120 = (57+63) = (40+80); (33+27) = 120:2; 3х120 = 360; | ||||||||
| Вид (тип) Лимбов NU – абриса: |
«L»
NU-1
|
«//»
NU-2 |
«Д»
NU-3
|
«//»
NU-4
|
«L»
NU-5
|
«&»
NU-6
|
«L»
NU-7
|
«L»
NU-8
|
«&»
NU-9
|
| Комбинации групп по «весу» = 120 |
(1 и 7), (2 и 4), 3, 6, 9, (5 и 8) х 2 | ||||||||
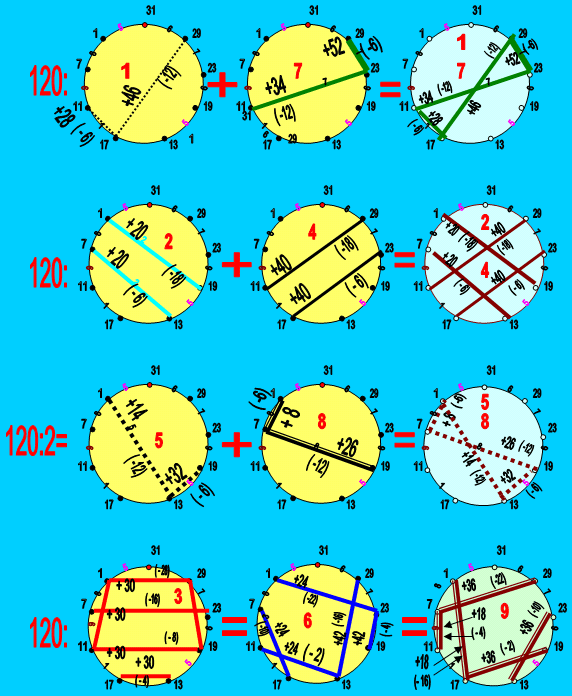
Объединение абрисов на «NU» - лимбах по принципу суммарного «веса» (Const = 120) группируемых чисел - участников
 |