Нумерология
О Единичности
Что может являться всеобъемлющим выражением Единичности? Этот или подобный вопрос рано или поздно возникает у всех, кто изучает эзотерические знания, оккультизм и символику. Примеров символа Единичности история знает предостаточно, но что касается обоснований, то с этим хуже…
В лучшем случае эти обоснования столь же эзотеричны, как и сам объект описания.
А нельзя ли получить такого рода обоснование из чисел или из математики?
Толчком к этой мысли послужило изучение свойств известной теоремы Пифагора о треугольнике.
Рассмотрим знаменитый треугольник Пифагора и связанные с ним формулы.
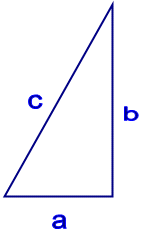 |
Общая формула, описывающая связь трёх сторон треугольника гласит, что: c2 = а2 +b2 .
Формулу можно преобразовать к виду: 1 = (а2/ c2 + b2/ c2)
Слагающие правой части формулы это ничто иное, как квадраты синуса и косинуса угла «альфа»:
1 а2/ c2 = Sin2 «альфа»
b2/ c2 = Cos2 «альфа»
Sin2 «альфа» + Cos2 «альфа» = 1
Отсюда следует вывод, что треугольник Пифагора олицетворяет собой просто-напросто ЕДИНИЦУ.
Однако, это не примитивное отождествление, так как содержит в себе ряд действий над числами, выражающих стороны треугольника ЧИСЛАМИ.
Здесь есть сложение, деление, возведение в степень, уравнивание, а также тригонометрические образы действия.
И только всё это в целом (числа и действия с ними!) ФОРМИРУЕТ собой ЕДИНИЦУ.
Более того, «формула Единичности» даёт нам намёк на механизм получения (?) СВОЙСТВА ЕДИНИЧНОСТИ из ТРЁХ составляющих, т.е. из ТРИАДЫ!
Если теперь вспомнить о том, какое внимание сам Пифагор уделял целочисленным значениям сторон своего треугольника, то станет понятно, что это не может быть случайным.
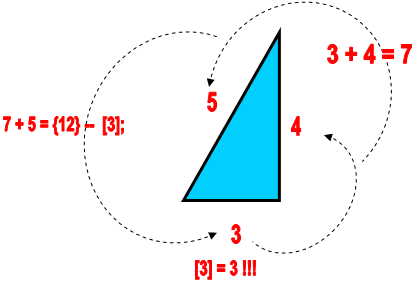
Вначале обратим внимание на то, что в треугольнике Пифагора (3,4,5) последовательное сложение сумм длин его сторон нумерологически совершает полный круг, то есть обход треугольника «возвращает» нас к исходному числу. Таким образом, как бы подчёркивая неизменность этой фигуры, её уникальность и Еденичность. Это иллюстрирует картинка внизу.
 |
Кроме того, если стороны равны числам 3, 4, 5, то определёнными ПРОСТЫМИ манипуляциями только с этими исходными цифрами можно получить следующие результаты:
4 – 3 = 1;
5 – 3 = 2;
3;
4;
5;
3 + 4 = 7;
3 + 5 = 8;
4 + 5 = 9;
===================================
(5 – 4) = (4 –3) = 1; 5 + (4 - 3) = 6?;
А вот, самая странная загадка состоит в том, что только цифра «6» !!!.... не получается также просто, как остальные цифры L ….
Спрашивается, а почему? Ведь число 6 пифагорейцы относили к т.н. «совершенным» числам!?
А вот, возможный ответ: Если мы возьмём и умножим все стороны знаменитого пифагорова треугольника, то получим следующее – 3 х 4 х 5 = 60.
То есть мы всё же получили число 6, но в интересной форме.
Наш результат 60 = 6 х 10;
А число 10 (Декада) у пифагорейцев было самым совершенным числом, которым они клялись! Так что получается, что Пифагоров треугольник содержит не одну, а целых три тайны:
Тайну Единого в Троичности (Единичности)
Тайну кругооборота в Едином Троичном
Тайну Совершенного в Совершенном (число 60!)