новая нумерология
Исследование взаимодействия цифр в числе
В данном исследовании мы будем рассматривать, описывать и анализировать взаимосвязи цифр внутри трёхзначных (трёхпозиционных) чисел. По традиции первый разряд (и соответствующую цифру) будем полагать старшим, а самую последнюю цифру – разряд будем считать самым младшим разрядом.
Для проведения исследования мы воспользуемся преобразованной нумерологически таблицей Пифагора (таблицей умножения), в которой каждый из столбцов будет являться кодовой последовательностью «цифр-позиций», которые отражают соответствующие Первоцифры.
| ТАБЛИЦА ПИФАГОРА (нумерологическая) | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 4 | 6 | 8 | 1 | 3 | 5 | 7 | 9 |
| 3 | 6 | 9 | 3 | 6 | 9 | 3 | 6 | 9 |
| 4 | 8 | 3 | 7 | 2 | 6 | 1 | 5 | 9 |
| 5 | 1 | 6 | 2 | 7 | 3 | 8 | 4 | 9 |
| 6 | 3 | 9 | 6 | 3 | 9 | 6 | 3 | 9 |
| 7 | 5 | 3 | 1 | 8 | 6 | 4 | 2 | 9 |
| 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 9 |
| 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
Это отображение в виде кодов (рядов) саморепликаций имеет смысл индивидуальных траекторий внутреннего самодвижения Первоцифр, закономерной смены «обликов исходной Первоцифры в ходе её самодвижения.
 |
 |
 |
 |
 |
 |
 |
 |
 |
Именно поэтому (при изучении чисел) удобно заменять одиночные Первоцифры чисел соответствующими кодами с тем, чтобы попытаться найти закономерности внутреннего взаимодействия цифр в математически едином нерасщепляемом далее числе.
| ЧИСЛО 317 |
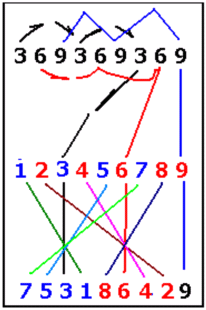 |
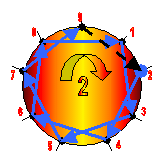
Проведены связи между одинаковыми цифрами-позициями в кодах саморепликации Первоцифр, входящих в исследуемое число 137. Цифры «смазки»- (3,6,9) присутствуют во всех цифрах, слагающих число 137
Выявлена группировка цифр кода саморепликации Первоцифры "7".
Цифры-позиции кода "1" спроецировались в коде "7". Причем, в две группы: нечётные в первую группу А, а чётные - во вторую группу - В.
Порядок проектирования (трансформации) – обратный, т.е. первая, нечётная позиция кода «цифры 1» стала последней позицией во второй группе саморепликационного кода цифры «7», а первая четная позиция кода "1" - последней позицией во второй группе кода цифры "7"..
Последующие позиции кода "1" (в порядке чтения - слева-направо) занимают позиции кода цифры "7" (по упомянутым подгруппам) в обратной последовательности, т. е. левее позиций, которые уже были заняты.
Позиции кода цифры "3" влияния на указанную закономерность НЕ оказали, так как в позициях кода "1" позиции цифры "3" следуют в том же порядке, что и в коде "1", а именно, стоят на З, 6, и 9 местах.
Таким образом, проецирование позиций кода цифры «3» не изменило естественный порядок следования (иерархии) на проецируемом коде цифры "1".
Всю картину можно условно уподобить последовательным проецированием (сверху - вниз).
Если иерархический код первой цифры числа не нарушается порядком следования (иерархией) второй цифры, то проецирование происходит 1 к 1.
Так имеет место при проектировании "3" à "1". В случае проектирования "1" à "7" иерархия последней, младшей цифры ("7") отличается по позициям соответствующих кодов саморепликаций этих цифр. В результате этого имеет место (наблюдается)
Перегруппировка позиций кода перегруппируемой цифры («1») в структуре кода перегруппируемой, младшей цифры («7»).
В данном случае эта перегруппировка (см. выше) содержала операции различения чётных и нечётных цифр-позиций в кодах, группировку и обратный прядок отображения в группах при проецировании позиций кода цифры "1" в позиции групп кода цифры "7"
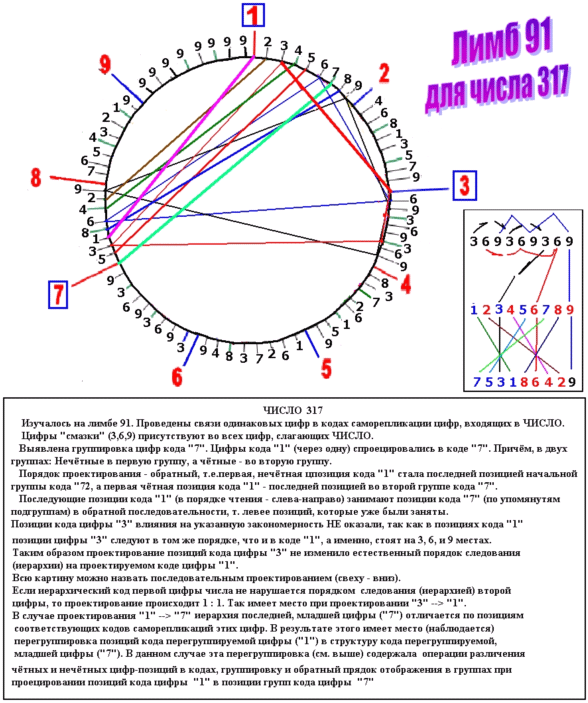 |
На данном рисунке – «Бланк исследования (пример) с лимбом – 91»
Число 371
 |
| Рис. 1 |
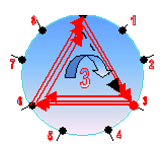
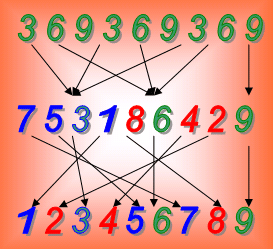
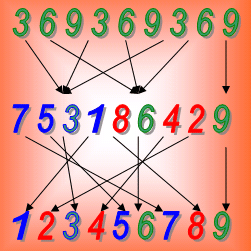
На данном рисунке (см. выше) представлена картина трансформации кодов цифр, составляющего число «371» в порядке уменьшения старшинства (иерархии) его цифровых позиций.
Число 317 представлено в вертикальном виде (кодами саморепликации входящих в него цифр). Верхний код – старшая цифра «3» (и её код) исследуемого числа.
- Как и в числе «317» можно видеть, что во всех трёх кодах позиции «чисел-смазок» 3,6,9) неизменны. И эти позиции не трансформируются, а прямо отражаются сверху – вниз без изменения.
- С позиции чёта – нечёта у нас получается картинка, которую можно выразить таблицей (см. ниже):
 |
| Рис. 2 |
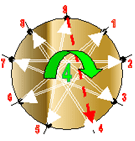
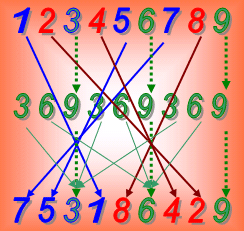
Если, как в предыдущем случае, как с числом «317» рассматривать связи саморепликационных кодов цифр числа «371, как трансформацию, то данное число примечательно тем, что взаимодействие кодов цифр «3» и «7» порождает код цифры «1», т.е. отрезок первых цифр натурального ряда.- (1,2,3,4,5,6,7,8,9).
Здесь мы можем видеть, как нейтральные цифры-позиции (3,6,9) свободно проецируются в код младшей цифры (1).
Здесь также наблюдаются две формирующиеся группировки (см. узлы пересекающихся связей одноимённых позиций). Однако, закономерности построения позиций младшего кода здесь иные, чем в первом примере (см. число «317»)..
Во-первых, эти две группы пересекаются и налагаются друг на друга.
Во-вторых, кроме позиции = 9, в коде среднего ранга, из всех позиций-цифр, чётко можно выделить первую группу (7531) и вторую (8642) группу..
Именно позиции-цифры этих групп далее трансформируются, т.е. изменяют порядок своего следования, своё позиционное место.
В группе А (7531) две первые цифры (7 и 5), а в группе В (8642) две последние цифры
(4 и 2) вторгаются (крест на крест) в порядок позиционирования кода итоговой цифры «1», код которой – [1234] [5678] (9).
Как можно видеть по расцветке цифр, последняя цифра-позиция группы А становится первой цифрой в младшем коде цифры «1», а первая цифра-позиция в группе В – становится последней позицией младшего кода цифры «1».
Свои законные места в младшем коде занимают цифры позиции – 3,6,9.
А вои «цифры – вторженцы» среднего кода (цифры 72) из первой группы А /7 и 5/, как уже говорилось, переходят во вторую группу кода младшей цифры, меняются местами и обрамляют соответствующие нейтральные цифры позиции. Здесь – цифру-позицию – 6.
Тоже самое происходит и с «цифрами – вторженцами» из второй группы В /2 и 4/; они обрамляют, поменявшись местами, нейтральную цифру-позицию – 3.
В сущности говоря, весь процесс трансформации кодов цифр, входящих в состав числа 371, от старшего кода числа (цифры 3) через код цифры 7 к коду цифры 1 напоминает сложение. Поскольку 3 +7 = {10}à [1]; То есть цифры –позиции кодов двух старших разрядов числа 371 преобразуются так, чтобы суммарный код младшей цифры был равен эквивалентной цифре = 1.
Теперь усложним задачу анализом следующего числа – изонума, а именно числа 137.
ЧИСЛО 137
 |
| Рис. 3 |
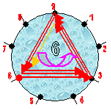
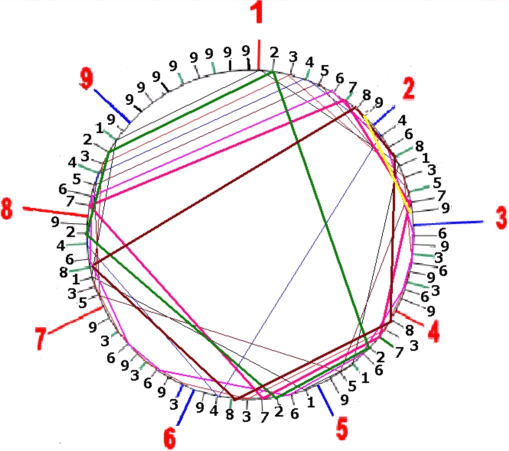
Анализ числа 137 (см. рис 4.) позволяет выявить следующие моменты:
К сожалению нельзя уподобить итоговую трансформацию кодов цифр данного числа, как это было сделано с числом 731, операции сложения двух старших кодов для получения кода младшего разряда, т.е. кода цифры «7». Ибо 1+3 = 4, а не 7 (!).
Тем не менее, коды как то трансформируются, что мы и наблюдаем на рисунке.
Рисунок заставляет нас предполагать, что в сущности код средней цифры «3» фактически не оказывает ЯВНОГО влияния на трансформацию кода старшей цифры " 1 " в " 7 "!.
Мы снова (в третий раз) убеждаемся, что цифры-позиции среднего кода (3,6,9,3,6,9,3,6,9), названные мной в рабочем порядке - «цифрами - смазками» (или нейтральными цифрами) фактически не участвуют в формировании итога.
Перегруппировки осуществляются, как бы, сквозь код средней цифры числа.
Снова в итоговом коде (в цифре 7) появляются две группы: А: (7531) и В: (8642), которые на этот раз сразу можно определить, как группу нечётных цифр-позиций (7531) и группу чётных цифр-позиций (8642).
Вполне отчётливо видно (см. рисунок), что идёт трансформация именно по признаку разделения чётных цифр-позиций от нечётных. При этом надо отметить, что на этот раз в процессе естественным образом вовлечены и нейтральные цифры-позиции, т.к. они заняли в итоговом коде своё законное проективное положение (!).
То есть, они как бы прямо и не участвуют в трансформации, но, в то же время, удачно вписались в описываемый здесь «алгоритм селекции», оказавшись как раз в нужном месте.
В целом, в данном опыте, как и в предыдущих опытах, можно наблюдать снова ДВЕ группы «цифр-позиций» формирующихся в коде младшей цифры числа 137 и прямое проектирование нейтральных цифр–позиций (3,6,9).в младший код цифры «7».
 |
| Рис. 4 |
|
Можно вывести одно точное определение относительно Первоцифр. После нумерологического сокращения таблицы Пифагора мы и имеем дело с трёхзначными числами и представляем входящие в них цифры - кодами саморепликации (этих самых цифр). Для этого случая установлено, что на 3, 6 и 9 позициях кодов любых Первоцифр всегда размещаются т. н. нейтральные цифры-позиции, которые либо вообще не влияют на процесс трансформации, либо оказываются в (итоге) в нужном месте итогового, младшего саморепликационного кода цифр-позиций. |